AndroidNote/CustomView/Advance/[9]Matrix_Basic.md

Matrix基础篇

目录

• Matrix简介
  • 概述
  • 常见误解
• Matrix详解

---

## Matrix简介

**Matrix是一个矩阵，主要功能是坐标映射，数值转换。**

它看起来大概是下面这样:

![](http://latex.codecogs.com/png.latex?

\\left [ 
\\begin{matrix} 
MSCALE\\_X & MSKEW\\_X & MTRANS\\_X \\\\
\\\\
MSKEW\\_Y & MSCALE\\_Y & MTRANS\\_Y \\\\
\\\\
MPERSP\\_0 & MPERSP\\_1 & MPERSP\\_2 
\\end{1} 
\\right ] 
$$)

下面我们看一下2D画布中常用的四种操作(translate, scale, rotate, skew)都是由哪些参数控制的。

![](http://ww2.sinaimg.cn/large/005Xtdi2jw1f60gwrhlnyj30c008zdgy.jpg)
![](http://ww2.sinaimg.cn/large/005Xtdi2jw1f633hvklfnj30c008zdge.jpg)

**从上图可以看到最后三个参数是控制透视的，这三个参数主要在3D效果中运用，通常为(0, 0, 1)，不在本篇讨论范围内，暂不过多叙述，会在之后对文章中详述其作用。**

<p id="wujie" /> 
### 常见误解

**1.认为Matrix最下面的一行的三个参数(MPERSP_0、MPERSP_1、MPERSP_2)没有什么太大的作用，在这里只是为了凑数。**

实际上最后一行参数在3D变换中有着至关重要的作用，这一点会在后面中Camera一文中详细介绍。

**2.最后一个参数MPERSP_2被解释为scale**

的确，更改MPERSP_2的值能够达到类似缩放的效果，但这是因为齐次坐标的缘故，并非这个参数的实际功能。

******

<p id="xiangjie" /> 
## Matrix详解

Matrix 是一个矩阵，最根本的作用就是坐标转换，下面我们就看看几种常见变换的原理:

常见的基本变换有4种: 平移(translate)、缩放(scale)、旋转(rotate) 和 错切(skew)。

由于我们以下大部分的计算都是基于矩阵乘法规则，如果你已经把线性代数还给了老师，请参考一下这里:
**[维基百科-矩阵乘法](https://zh.wikipedia.org/wiki/%E7%9F%A9%E9%99%A3%E4%B9%98%E6%B3%95)**

### 1.缩放

![](http://latex.codecogs.com/png.latex?$$ x = k_1 x_0 $$)

![](http://latex.codecogs.com/png.latex?$$ y = k_2 y_0 $$)


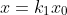
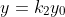
用矩阵表示: 

![](http://latex.codecogs.com/png.latex?

\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix} k_1 & 0 & 0 \\ 0 & k_2 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0 \\ y_0 \\ 1 \end{1} \right ]

)

> 
你可能注意到了，我们坐标多了一个1，这是使用了齐次坐标系的缘故，在数学中我们的点和向量都是这样表示的(x, y)，两者看起来一样，计算机无法区分，为此让计算机也可以区分它们，增加了一个标志位，增加之后看起来是这样: <br/>
>
(x, y, 1) - 点<br/>
(x, y, 0) - 向量<br/>
>
另外，齐次坐标具有等比的性质，(2,3,1)、(4,6,2)...(2N,3N,N)表示的均是(2,3)这一个点。(**将MPERSP_2解释为scale这一误解就源于此**)。

图例：

![](http://ww1.sinaimg.cn/large/005Xtdi2jw1f6cnk02zy9j308c0dwwej.jpg)

### 2.错切

错切存在两种特殊错切，水平错切(平行X轴)和垂直错切(平行Y轴)。

#### 水平错切

![](http://latex.codecogs.com/png.latex?$$ x = x + ky_0 $$)

![](http://latex.codecogs.com/png.latex?$$ y = y_0 $$)

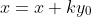
用矩阵表示:

![](http://latex.codecogs.com/png.latex?

\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix}
1 & k & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]

)

图例:

![](http://ww2.sinaimg.cn/large/005Xtdi2jw1f6cniifb0sj308c0dw3yz.jpg)

### 3.旋转

逆时针旋转 a 度。

![](http://latex.codecogs.com/png.latex?

\left [ \begin{matrix} x\\ y 1 \end{1} \right ]

\left [ \begin{matrix} cos(a) & -sin(a) & 0 \\ sin(a) & cos(a) & 0 \\ 0 & 0 & 1 \end{1} \right ] . \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]

)


### 4.平移

![](http://latex.codecogs.com/png.latex?$$ x = x_0 + \\Delta x $$)

![](http://latex.codecogs.com/png.latex?$$ y = y_0 + \\Delta y $$)


![](http://latex.codecogs.com/png.latex?

\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ]

\left [ \begin{matrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{1} \right ] . \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]

)









**Matrix方法表**

方法类别   | 相关API                                                 | 摘要
-----------|---------------------------------------------------------|------------------------
基本方法   | equals hashCode toString toShortString                  | 比较、 获取哈希值、 转换为字符串
数值操作   | set reset setValues getValues                           | 设置、 重置、 设置数值、 获取数值
数值计算   | mapPoints mapRadius mapRect mapVectors                  | 计算变换后的数值
设置(set)  | setConcat setRotate setScale setSkew setTranslate       | 设置变换
前乘(pre)  | preConcat preRotate preScale preSkew preTranslate       | 前乘变换
后乘(post) | postConcat postRotate postScale postSkew postTranslate  | 后乘变换
特殊方法   | setPolyToPoly setRectToRect rectStaysRect setSinCos     | 一些特殊操作
矩阵相关   | invert isAffine isIdentity                              | 求逆矩阵、 是否为仿射矩阵、 是否为单位矩阵 ...