Update
This commit is contained in:
@@ -1 +1,105 @@
|
||||
# Path之贝塞尔曲线
|
||||
|
||||
### 作者微博: [@攻城师sloop](http://weibo.com/GcsSloop)
|
||||
|
||||
本次讲解Path中的贝塞尔曲线部分,创造更多**炫(zhuang)酷(B)**的东东。
|
||||
|
||||
******
|
||||
|
||||
# 一.Path常用方法表
|
||||
> 为了兼容性(_偷懒_) 本表格中去除了在API21(即安卓版本5.0)以上才添加的方法。忍不住吐槽一下,为啥看起来有些顺手就能写的重载方法要等到API21才添加上啊。宝宝此刻内心也是崩溃的。
|
||||
|
||||
作用 | 相关方法 | 备注
|
||||
--- | --- | ---
|
||||
移动起点 | moveTo | 移动下一次操作的起点位置
|
||||
设置终点 | setLastPoint | 重置当前path中最后一个点位置,如果在绘制之前调用,效果和moveTo相同
|
||||
连接直线 | lineTo | 添加上一个点到当前点之间的直线到Path
|
||||
闭合路径 | close | 连接第一个点连接到最后一个点,形成一个闭合区域
|
||||
添加内容 | addRect, addRoundRect, addOval, addCircle, addPath, addArc, arcTo | 添加(矩形, 圆角矩形, 椭圆, 圆, 路径, 圆弧) 到当前Path (注意addArc和arcTo的区别)
|
||||
是否为空 | isEmpty | 判断Path是否为空
|
||||
是否为矩形 | isRect | 判断path是否是一个矩形
|
||||
替换路径 | set | 用新的路径替换到当前路径所有内容
|
||||
偏移路径 | offset | 对当前路径之前的操作进行偏移(不会影响之后的操作)
|
||||
贝塞尔曲线 | quadTo, cubicTo | 分别为二次和三次贝塞尔曲线的方法
|
||||
rXxx方法 | rMoveTo, rLineTo, rQuadTo, rCubicTo | **不带r的方法是基于原点的坐标系(偏移量),rXxx方法是基于当前点坐标系(偏移量)**
|
||||
填充模式 | setFillType, getFillType, isInverseFillType, toggleInverseFillType| 设置,获取,判断和切换填充模式
|
||||
提示方法 | incReserve | 提示Path还有多少个点等待加入**(这个方法貌似会让Path优化存储结构)**
|
||||
布尔操作(API19) | op | 对两个Path进行布尔运算(即取交集、并集等操作)
|
||||
计算边界 | computeBounds | 计算Path的边界
|
||||
重置路径 | reset, rewind | 清除Path中的内容(**reset相当于重置到new Path阶段,rewind会保留Path的数据结构**)
|
||||
矩阵操作 | transform | 矩阵变换
|
||||
|
||||
# 二.Path详解
|
||||
|
||||
上一次除了一些常用函数之外,讲解的基本上都是直线,本次需要了解其中的曲线部分,说到曲线,就不得不提大名鼎鼎的贝塞尔曲线。
|
||||
就是下面这个人(法国数学家PierreBézier)所发现的。
|
||||
|
||||
|
||||

|
||||
|
||||
**搜索贝塞尔曲线,我们看到的基本就是下面这些不明觉厉的图形:**
|
||||
|
||||
贝塞尔曲线 | 结构 | 演示动画
|
||||
--- | --- | ---
|
||||
一阶曲线<br/>(线性曲线) |  | 
|
||||
二阶曲线 |  | 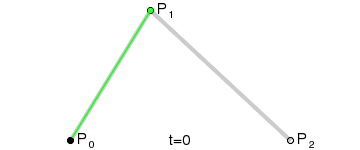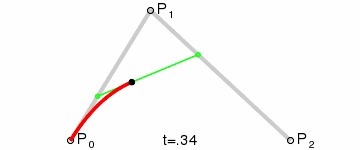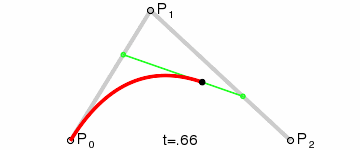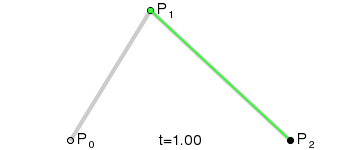
|
||||
三阶曲线 |  | 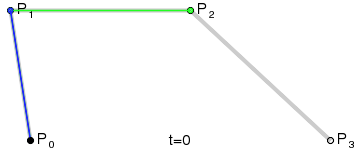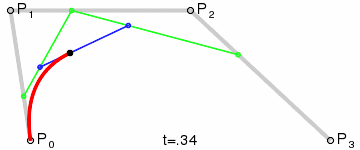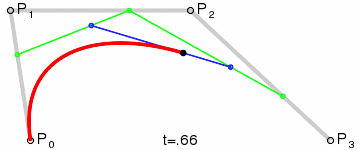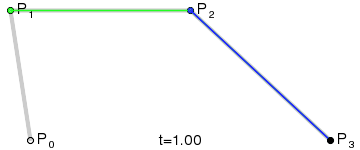
|
||||
四阶曲线 |  | 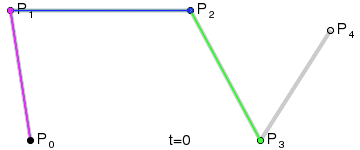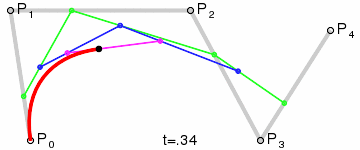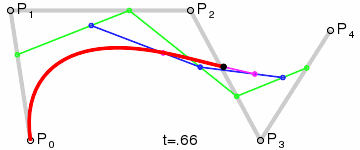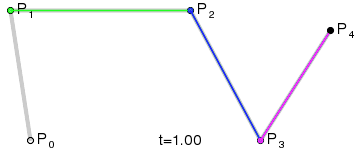
|
||||
|
||||
**或者类似于这样的不明觉厉的公式:**
|
||||
|
||||

|
||||
|
||||
**话说这根本就是数学家干的活吧,让我一个写程序(_差点挂在高数上下不来_)的弄这个?**
|
||||
|
||||
<img src = "http://ww4.sinaimg.cn/large/005Xtdi2jw1f1ko2ld47aj309c0aajrp.jpg" width=168 height = 185/>
|
||||
|
||||
不过嘛,不用担心,本次内容中不会拿这些不明觉厉的公式去忽悠大家,下面正式开始。
|
||||
|
||||
## 贝塞尔曲线能干什么?
|
||||
|
||||
额,一个比较弱智的问题,人家都说是曲线了,肯定就是画曲线啦,不然还能干什么!
|
||||
|
||||
例如绘制一个妹子的小蛮腰。:point_down:
|
||||
|
||||
**:warning:前方高能预警,非战斗人员请迅速撤离!!!**
|
||||
|
||||
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>><br/>
|
||||
|
||||

|
||||
|
||||
**如果没有贝塞尔曲线,就会变成这样子。:point_down:**
|
||||
|
||||

|
||||
|
||||
<br/>
|
||||
|
||||
贝塞尔曲线的运用是十分广泛的,可以说**贝塞尔曲线奠定了计算机绘图的基础(_因为它可以将任何复杂的图形用精确的数学语言进行描述_)**,在你不经意间就已经使用过它了。
|
||||
|
||||
你会使用Photoshop的话,你可能会注意到里面有一个**钢笔工具**。这是一个令人十分费解的东西,我在一开始尝试使用的时候总会制造出一些和我预期不同的曲线,各种歪歪扭扭。这个钢笔工具就是贝塞尔曲线的一种运用。
|
||||
|
||||
你说你不会PS? 没关系,你如果看过前面的文章或者用过2D绘图,肯定绘制过圆,圆弧,圆角矩形等这些东西。这里面的圆弧部分全部都是贝塞尔曲线的运用。
|
||||
|
||||
实际上在前面我们所绘制的**圆是用四段贝塞尔曲线拼接出来的**,有木有觉得很不可思议?
|
||||
|
||||
相信很多人看到这里都会怀疑,因为上过中学的人都知道圆是有自己的方程式的,而且比贝塞尔曲线简单的多。
|
||||
|
||||
如果你们不相信的话,咱们可以做一个实验,**教大家如何用圆分分钟做出一个吃豆人**:
|
||||
|
||||
上代码:
|
||||
``` java
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 论如何避免接触公式学好贝塞尔曲线
|
||||
|
||||
|
||||
|
||||
|
||||
# 三.总结
|
||||
|
||||
# 四.参考资料
|
||||
|
||||
Reference in New Issue
Block a user