2016-07-23 01:18:44 +08:00
|
|
|
|
# Matrix基础篇
|
2016-06-06 17:39:12 +08:00
|
|
|
|
|
2016-08-02 03:40:57 +08:00
|
|
|
|
### 作者微博: [@GcsSloop](http://weibo.com/GcsSloop)
|
|
|
|
|
|
### [【本系列相关文章】](https://github.com/GcsSloop/AndroidNote/tree/master/CustomView/README.md)
|
|
|
|
|
|
|
2016-07-20 06:10:39 +08:00
|
|
|
|
|
2016-07-26 06:08:56 +08:00
|
|
|
|
## 目录
|
2016-07-23 01:31:39 +08:00
|
|
|
|
|
2016-08-01 07:01:24 +08:00
|
|
|
|
- [前言](#qianyan)
|
2016-07-26 06:13:17 +08:00
|
|
|
|
- [Matrix简介](#jianjie)
|
2016-08-01 06:47:35 +08:00
|
|
|
|
- [Matrix基本原理](#jiben)
|
|
|
|
|
|
- [Matrix复合原理](#fuhe)
|
2016-08-01 06:50:21 +08:00
|
|
|
|
- [Matrix方法表](#fangfa)
|
2016-08-02 03:45:46 +08:00
|
|
|
|
- [总结](#zongjie)
|
|
|
|
|
|
- [关于作者](#about)
|
|
|
|
|
|
- [参考资料](#ziliao)
|
2016-08-01 06:47:35 +08:00
|
|
|
|
|
2016-08-01 07:01:24 +08:00
|
|
|
|
<p id="qianyan" />
|
|
|
|
|
|
## 前言
|
|
|
|
|
|
|
|
|
|
|
|
本文内容偏向理论,和 [画布操作](https://github.com/GcsSloop/AndroidNote/blob/master/CustomView/Advance/%5B3%5DCanvas_Convert.md) 有重叠的部分,本文会让你更加深入的了解其中的原理。
|
|
|
|
|
|
|
|
|
|
|
|
由于Google已经对这一部分已经做了很好的封装,所以跳过本部分对实际开发影响并不会太大,不想深究的粗略浏览即可,下一篇中将会详细讲解Matrix的具体用法和技巧。
|
2016-07-20 17:05:00 +08:00
|
|
|
|
|
2016-07-23 01:15:22 +08:00
|
|
|
|
******
|
|
|
|
|
|
|
2016-07-26 06:13:17 +08:00
|
|
|
|
<p id="jianjie" />
|
2016-07-26 06:08:56 +08:00
|
|
|
|
## Matrix简介
|
2016-07-23 01:15:22 +08:00
|
|
|
|
|
2016-07-26 06:39:13 +08:00
|
|
|
|
<p id="gaishu" />
|
2016-07-26 06:08:13 +08:00
|
|
|
|
**Matrix是一个矩阵,主要功能是坐标映射,数值转换。**
|
2016-07-26 06:02:36 +08:00
|
|
|
|
|
|
|
|
|
|
它看起来大概是下面这样:
|
2016-07-22 04:01:04 +08:00
|
|
|
|
|
|
|
|
|
|

|
2016-06-10 02:41:55 +08:00
|
|
|
|
|
2016-07-26 06:02:36 +08:00
|
|
|
|
下面我们看一下2D画布中常用的四种操作(translate, scale, rotate, skew)都是由哪些参数控制的。
|
2016-07-20 04:04:36 +08:00
|
|
|
|
|
2016-07-20 16:48:25 +08:00
|
|
|
|

|
2016-07-22 23:21:08 +08:00
|
|
|
|

|
2016-07-20 04:04:36 +08:00
|
|
|
|
|
2016-07-26 06:18:07 +08:00
|
|
|
|
**从上图可以看到最后三个参数是控制透视的,这三个参数主要在3D效果中运用,通常为(0, 0, 1),不在本篇讨论范围内,暂不过多叙述,会在之后对文章中详述其作用。**
|
2016-07-20 04:04:36 +08:00
|
|
|
|
|
2016-08-02 02:44:03 +08:00
|
|
|
|
### Matrix优点
|
|
|
|
|
|
|
|
|
|
|
|
* 作用范围更广,Matrix在自定义View,图片,动画效果上均有运用,相比与之前讲对画布操作应用范围更广。
|
|
|
|
|
|
* 更加灵活,画布操作是对Matrix的封装,Matrix作为更接近底层的东西,必然要比画布操作更加灵活。
|
|
|
|
|
|
* 封装很好,Matrix本身对各个方法就做了很好的封装,让开发者可以很方便的操作Matrix。
|
|
|
|
|
|
|
|
|
|
|
|
### Matrix缺点
|
|
|
|
|
|
|
|
|
|
|
|
* 难以深入理解,很难理解中各个数值的意义,以及操作规律,如果不了解矩阵,也很难理解前乘,后乘。
|
|
|
|
|
|
|
2016-07-26 06:14:29 +08:00
|
|
|
|
<p id="wujie" />
|
2016-07-22 04:01:04 +08:00
|
|
|
|
### 常见误解
|
2016-07-21 04:09:29 +08:00
|
|
|
|
|
2016-07-21 04:14:15 +08:00
|
|
|
|
**1.认为Matrix最下面的一行的三个参数(MPERSP_0、MPERSP_1、MPERSP_2)没有什么太大的作用,在这里只是为了凑数。**
|
2016-07-21 04:09:29 +08:00
|
|
|
|
|
2016-07-26 06:18:07 +08:00
|
|
|
|
实际上最后一行参数在3D变换中有着至关重要的作用,这一点会在后面中Camera一文中详细介绍。
|
2016-07-21 04:09:29 +08:00
|
|
|
|
|
2016-07-21 17:15:35 +08:00
|
|
|
|
**2.最后一个参数MPERSP_2被解释为scale**
|
2016-07-21 04:09:29 +08:00
|
|
|
|
|
2016-07-26 06:18:07 +08:00
|
|
|
|
的确,更改MPERSP_2的值能够达到类似缩放的效果,但这是因为齐次坐标的缘故,并非这个参数的实际功能。
|
2016-07-21 04:09:29 +08:00
|
|
|
|
|
2016-07-26 06:14:29 +08:00
|
|
|
|
******
|
2016-07-21 04:09:29 +08:00
|
|
|
|
|
2016-08-01 06:47:35 +08:00
|
|
|
|
<p id="jiben" />
|
|
|
|
|
|
## Matrix基本原理
|
2016-07-22 07:26:20 +08:00
|
|
|
|
|
2016-07-26 06:18:07 +08:00
|
|
|
|
Matrix 是一个矩阵,最根本的作用就是坐标转换,下面我们就看看几种常见变换的原理:
|
2016-07-24 02:53:41 +08:00
|
|
|
|
|
2016-08-01 06:47:35 +08:00
|
|
|
|
> 我们所用到的变换均属于仿射变换,仿射变换是 线性变换(缩放,旋转,错切) 和 平移变换(平移) 的复合,由于这些概念对于我们作用并不大,此处不过多介绍,有兴趣可自行了解。
|
|
|
|
|
|
|
|
|
|
|
|
基本变换有4种: 平移(translate)、缩放(scale)、旋转(rotate) 和 错切(skew)。
|
2016-07-24 03:17:36 +08:00
|
|
|
|
|
2016-07-26 06:02:36 +08:00
|
|
|
|
由于我们以下大部分的计算都是基于矩阵乘法规则,如果你已经把线性代数还给了老师,请参考一下这里:
|
2016-07-24 03:17:36 +08:00
|
|
|
|
**[维基百科-矩阵乘法](https://zh.wikipedia.org/wiki/%E7%9F%A9%E9%99%A3%E4%B9%98%E6%B3%95)**
|
2016-07-24 02:57:06 +08:00
|
|
|
|
|
2016-08-01 02:00:17 +08:00
|
|
|
|
### 1.缩放(Scale)
|
2016-07-24 02:33:08 +08:00
|
|
|
|
|
2016-07-29 23:20:33 +08:00
|
|
|
|
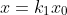
|
|
|
|
|
|
|
|
|
|
|
|
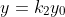
|
2016-07-27 04:44:59 +08:00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
用矩阵表示:
|
2016-07-24 03:06:46 +08:00
|
|
|
|
|
2016-07-24 03:17:36 +08:00
|
|
|
|

|
|
|
|
|
|
|
2016-07-27 05:31:57 +08:00
|
|
|
|
>
|
|
|
|
|
|
你可能注意到了,我们坐标多了一个1,这是使用了齐次坐标系的缘故,在数学中我们的点和向量都是这样表示的(x, y),两者看起来一样,计算机无法区分,为此让计算机也可以区分它们,增加了一个标志位,增加之后看起来是这样: <br/>
|
|
|
|
|
|
>
|
|
|
|
|
|
(x, y, 1) - 点<br/>
|
|
|
|
|
|
(x, y, 0) - 向量<br/>
|
|
|
|
|
|
>
|
|
|
|
|
|
另外,齐次坐标具有等比的性质,(2,3,1)、(4,6,2)...(2N,3N,N)表示的均是(2,3)这一个点。(**将MPERSP_2解释为scale这一误解就源于此**)。
|
|
|
|
|
|
|
2016-07-31 03:49:17 +08:00
|
|
|
|
图例:
|
|
|
|
|
|
|
2016-07-31 05:44:38 +08:00
|
|
|
|

|
2016-07-31 03:49:17 +08:00
|
|
|
|
|
2016-08-01 02:00:17 +08:00
|
|
|
|
### 2.错切(Skew)
|
2016-07-24 15:58:35 +08:00
|
|
|
|
|
2016-07-31 03:21:14 +08:00
|
|
|
|
错切存在两种特殊错切,水平错切(平行X轴)和垂直错切(平行Y轴)。
|
|
|
|
|
|
|
|
|
|
|
|
#### 水平错切
|
|
|
|
|
|
|
2016-07-31 05:47:58 +08:00
|
|
|
|

|
2016-07-31 03:21:14 +08:00
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
用矩阵表示:
|
2016-07-26 04:36:27 +08:00
|
|
|
|
|
2016-07-26 04:20:03 +08:00
|
|
|
|

|
|
|
|
|
|
|
2016-07-31 05:44:38 +08:00
|
|
|
|
图例:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
2016-07-31 05:47:58 +08:00
|
|
|
|
#### 垂直错切
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
用矩阵表示:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
图例:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
2016-07-31 07:22:27 +08:00
|
|
|
|
#### 复合错切
|
|
|
|
|
|
|
|
|
|
|
|
> 水平错切和垂直错切的复合。
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
用矩阵表示:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
2016-07-31 07:23:01 +08:00
|
|
|
|
图例:
|
|
|
|
|
|
|
|
|
|
|
|

|
2016-07-31 07:22:27 +08:00
|
|
|
|
|
2016-08-01 02:00:17 +08:00
|
|
|
|
### 3.旋转(Rotate)
|
2016-07-26 04:37:19 +08:00
|
|
|
|
|
2016-07-31 06:57:02 +08:00
|
|
|
|
假定一个点 A(x<sub>0</sub>, y<sub>0</sub>) ,距离原点距离为 r, 与水平轴夹角为 α 度, 绕原点旋转 θ 度, 旋转后为点 B(x, y) 如下:
|
|
|
|
|
|
|
|
|
|
|
|
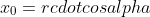
|
|
|
|
|
|
|
|
|
|
|
|
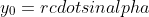
|
|
|
|
|
|
|
2016-07-31 07:08:37 +08:00
|
|
|
|

|
|
|
|
|
|
= r \\cdot cos \\alpha \\cdot cos \\theta - r \\cdot sin \\alpha \\cdot sin \\theta
|
|
|
|
|
|
= x_0 \\cdot cos \\theta - y_0 \\cdot sin \\theta
|
|
|
|
|
|
$$)
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
= r \\cdot sin \\alpha \\cdot cos \\theta + r \\cdot cos \\alpha \\cdot sin \\theta
|
|
|
|
|
|
= y_0 \\cdot cos \\theta + x_0 \\cdot sin \\theta
|
|
|
|
|
|
$$)
|
|
|
|
|
|
|
2016-07-31 07:10:41 +08:00
|
|
|
|
用矩阵表示:
|
2016-07-26 05:13:51 +08:00
|
|
|
|
|
|
|
|
|
|
 & -sin(\\theta) & 0 \\\\
|
|
|
|
|
|
sin(\\theta) & cos(\\theta) & 0 \\\\
|
|
|
|
|
|
0 & 0 & 1
|
2016-07-26 05:13:51 +08:00
|
|
|
|
\\end{1}
|
|
|
|
|
|
\\right ]
|
|
|
|
|
|
.
|
|
|
|
|
|
\\left [
|
|
|
|
|
|
\\begin{matrix}
|
2016-07-28 04:48:35 +08:00
|
|
|
|
x_0\\\\
|
|
|
|
|
|
y_0\\\\
|
|
|
|
|
|
1
|
2016-07-26 05:13:51 +08:00
|
|
|
|
\\end{1}
|
|
|
|
|
|
\\right ]
|
|
|
|
|
|
$$)
|
|
|
|
|
|
|
2016-07-31 07:10:41 +08:00
|
|
|
|
图例:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
2016-08-01 02:00:17 +08:00
|
|
|
|
### 4.平移(Translate)
|
2016-07-26 04:37:19 +08:00
|
|
|
|
|
2016-08-01 06:47:35 +08:00
|
|
|
|
>
|
|
|
|
|
|
此处也是使用齐次坐标的优点体现之一,实际上前面的三个操作使用 2x2 的矩阵也能满足需求,但是使用 2x2 的矩阵,无法将平移操作加入其中,而将坐标扩展为齐次坐标后,将矩阵扩展为 3x3 就可以将算法统一,四种算法均可以使用矩阵乘法完成。
|
|
|
|
|
|
|
2016-07-29 22:50:40 +08:00
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
2016-08-01 02:00:17 +08:00
|
|
|
|
用矩阵表示:
|
2016-07-29 22:50:40 +08:00
|
|
|
|
|
2016-07-29 01:39:19 +08:00
|
|
|
|

|
2016-07-22 02:47:02 +08:00
|
|
|
|
|
2016-08-01 04:13:34 +08:00
|
|
|
|
图例:
|
2016-07-22 02:47:02 +08:00
|
|
|
|
|
2016-08-01 04:13:34 +08:00
|
|
|
|

|
2016-07-22 02:47:02 +08:00
|
|
|
|
|
2016-07-21 04:09:29 +08:00
|
|
|
|
|
2016-08-01 06:47:35 +08:00
|
|
|
|
<p id="fuhe" />
|
|
|
|
|
|
## Matrix复合原理
|
2016-07-20 17:05:00 +08:00
|
|
|
|
|
2016-08-02 00:40:48 +08:00
|
|
|
|
其实Matrix的多种复合操作都是使用矩阵乘法实现的,从原理上理解很简单,但是,使用矩阵乘法也有其弱点,后面的操作可能会影响到前面到操作,所以在构造Matrix时顺序很重要。
|
|
|
|
|
|
|
2016-08-02 00:58:57 +08:00
|
|
|
|
我们常用的四大变换操作,每一种操作在Matrix均有三类,前乘(pre),后乘(post)和设置(set),可以参见文末对[Matrix方法表](#fangfa),由于矩阵乘法不满足交换律,所以前乘(pre),后乘(post)和设置(set)的区别还是很大的。
|
|
|
|
|
|
|
|
|
|
|
|
### 前乘(pre)
|
|
|
|
|
|
|
|
|
|
|
|
前乘相当于矩阵的右乘:
|
|
|
|
|
|
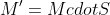
|
|
|
|
|
|
|
|
|
|
|
|
> 这表示一个矩阵与一个特殊矩阵前乘后构造出结果矩阵。
|
|
|
|
|
|
|
2016-08-02 02:17:27 +08:00
|
|
|
|
### 后乘(post)
|
2016-08-02 00:58:57 +08:00
|
|
|
|
|
2016-08-02 02:17:27 +08:00
|
|
|
|
前乘相当于矩阵的左乘:
|
|
|
|
|
|
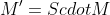
|
2016-08-02 00:40:48 +08:00
|
|
|
|
|
2016-08-02 02:17:27 +08:00
|
|
|
|
> 这表示一个矩阵与一个特殊矩阵后乘后构造出结果矩阵。
|
2016-07-20 04:04:36 +08:00
|
|
|
|
|
2016-08-02 02:17:27 +08:00
|
|
|
|
### 设置(set)
|
2016-07-20 01:45:13 +08:00
|
|
|
|
|
2016-08-02 02:44:03 +08:00
|
|
|
|
设置使用的不是矩阵乘法,而是直接覆盖掉原来的数值,所以,**使用设置可能会导致之前的操作失效**。
|
2016-07-20 01:45:13 +08:00
|
|
|
|
|
2016-08-02 03:24:34 +08:00
|
|
|
|
## 组合
|
|
|
|
|
|
|
|
|
|
|
|
我们使用Matrix最终目的就是让视图显示为我们想要的状态,为此我们可能需要多种操作结合使用。
|
|
|
|
|
|
|
|
|
|
|
|
我发现很多讲解Matrix的文章喜欢用绕某一个点缩放(旋转)的示例来讲解,如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>
|
|
|
|
|
|
那么我们如果想让它基于图片中心缩放,应该该怎么办?要用到组合变换,
|
|
|
|
|
|
1)先将图片由中心平移到原点,这是应用变换 T
|
|
|
|
|
|
2)对图应用缩放变换 S
|
|
|
|
|
|
3)再将图片平移回到中心,应用变换 -T
|
|
|
|
|
|
|
|
|
|
|
|
>
|
|
|
|
|
|
对应代码:
|
|
|
|
|
|
matrix.postScale(0.5f, 0.5f);
|
|
|
|
|
|
matrix.preTranslate(-pivotX, -pivotY);
|
|
|
|
|
|
matrix.postTranslate(pivotX, pivotY);
|
|
|
|
|
|
>
|
|
|
|
|
|
PS: 此段文字引用自其它文章。
|
|
|
|
|
|
|
|
|
|
|
|
首先,**这个思路是没有任何问题的,也是实现绕某一点操作的核心原理**,但这可能会对一部分小白造成误解,认为只能这样实现,然而查看一下Matrix的方法表就能知道四大操作都可以指定中心点,所以,上面的三行代码用一行就能完成:
|
|
|
|
|
|
|
|
|
|
|
|
```java
|
|
|
|
|
|
matrix.postScale(0.5f, 0.5f, pivotX, pivotY);
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
**组合操作构造Matrix时,个人建议尽量全部使用后乘或者全部使用前乘,这样操作顺序容易确定,出现问题也比较容易排查。<br/>当然,由于矩阵乘法不满足交换律,前乘和后乘的结果是不同的,使用时应结合具体情景分析使用。**
|
|
|
|
|
|
|
2016-08-01 07:01:24 +08:00
|
|
|
|
<p id="fangfa" />
|
2016-08-01 06:50:21 +08:00
|
|
|
|
## Matrix方法表
|
2016-07-21 03:09:37 +08:00
|
|
|
|
|
2016-08-02 03:29:22 +08:00
|
|
|
|
这个方法表,暂时放到这里让大家看看,方法的使用讲解放在下一篇文章中。
|
|
|
|
|
|
|
2016-07-21 03:09:37 +08:00
|
|
|
|
方法类别 | 相关API | 摘要
|
|
|
|
|
|
-----------|---------------------------------------------------------|------------------------
|
|
|
|
|
|
基本方法 | equals hashCode toString toShortString | 比较、 获取哈希值、 转换为字符串
|
2016-07-23 00:58:04 +08:00
|
|
|
|
数值操作 | set reset setValues getValues | 设置、 重置、 设置数值、 获取数值
|
|
|
|
|
|
数值计算 | mapPoints mapRadius mapRect mapVectors | 计算变换后的数值
|
2016-07-21 03:09:37 +08:00
|
|
|
|
设置(set) | setConcat setRotate setScale setSkew setTranslate | 设置变换
|
|
|
|
|
|
前乘(pre) | preConcat preRotate preScale preSkew preTranslate | 前乘变换
|
|
|
|
|
|
后乘(post) | postConcat postRotate postScale postSkew postTranslate | 后乘变换
|
|
|
|
|
|
特殊方法 | setPolyToPoly setRectToRect rectStaysRect setSinCos | 一些特殊操作
|
|
|
|
|
|
矩阵相关 | invert isAffine isIdentity | 求逆矩阵、 是否为仿射矩阵、 是否为单位矩阵 ...
|
|
|
|
|
|
|
2016-08-02 03:45:46 +08:00
|
|
|
|
<p id="zongjie" />
|
2016-08-02 03:40:57 +08:00
|
|
|
|
## 总结
|
2016-07-21 03:09:37 +08:00
|
|
|
|
|
2016-06-13 17:01:01 +08:00
|
|
|
|
|
2016-08-02 03:45:46 +08:00
|
|
|
|
<p id="about" />
|
2016-08-02 03:40:57 +08:00
|
|
|
|
## About Me
|
2016-06-13 17:01:01 +08:00
|
|
|
|
|
2016-08-02 03:40:57 +08:00
|
|
|
|
### 作者微博: [@GcsSloop](http://weibo.com/GcsSloop)
|
2016-06-13 17:01:01 +08:00
|
|
|
|
|
2016-08-02 03:40:57 +08:00
|
|
|
|
<a href="https://github.com/GcsSloop/AndroidNote/blob/magic-world/FINDME.md" target="_blank"> <img src="http://ww4.sinaimg.cn/large/005Xtdi2gw1f1qn89ihu3j315o0dwwjc.jpg" width=300 height=100 /> </a>
|
2016-06-13 17:01:01 +08:00
|
|
|
|
|
2016-08-02 03:45:46 +08:00
|
|
|
|
<p id="ziliao" />
|
2016-08-02 03:40:57 +08:00
|
|
|
|
## 参考资料
|
2016-06-13 17:01:01 +08:00
|
|
|
|
|
2016-08-02 03:53:39 +08:00
|
|
|
|
[Matrix](https://developer.android.com/reference/android/graphics/Matrix.html)<br/>
|
|
|
|
|
|
[Android中图像变换Matrix的原理、代码验证和应用](http://biandroid.iteye.com/blog/1399462)<br/>
|
|
|
|
|
|
[Android中关于矩阵(Matrix)前乘后乘的一些认识](http://blog.csdn.net/linmiansheng/article/details/18820599)<br/>
|
|
|
|
|
|
[维基百科-仿射变换](https://zh.wikipedia.org/wiki/%E4%BB%BF%E5%B0%84%E5%8F%98%E6%8D%A2)<br/>
|
|
|
|
|
|
[维基百科-齐次坐标](https://zh.wikipedia.org/wiki/%E9%BD%90%E6%AC%A1%E5%9D%90%E6%A0%87)<br/>
|
|
|
|
|
|
[维基百科-线性映射](https://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E6%98%A0%E5%B0%84)<br/>
|
|
|
|
|
|
[齐次坐标系入门级思考](https://oncemore2020.github.io/blog/homogeneous/)<br/>
|
|
|
|
|
|
[仿射变换与齐次坐标](https://guangchun.wordpress.com/2011/10/12/affineandhomogeneous/)<br/>
|
2016-08-02 03:40:57 +08:00
|
|
|
|
[]()<br/>
|