老师，请问共现矩阵奇异值分解后为什么是用U的行来做word embedding呢?

cs224n课程第一周里，提到了2种生成word embedding的方法。
一种是基于word2vec的神经网络生成词向量的方法。
另一种是基于统计的词向量生成的方法：使用共现矩阵，再进行SVD分解。

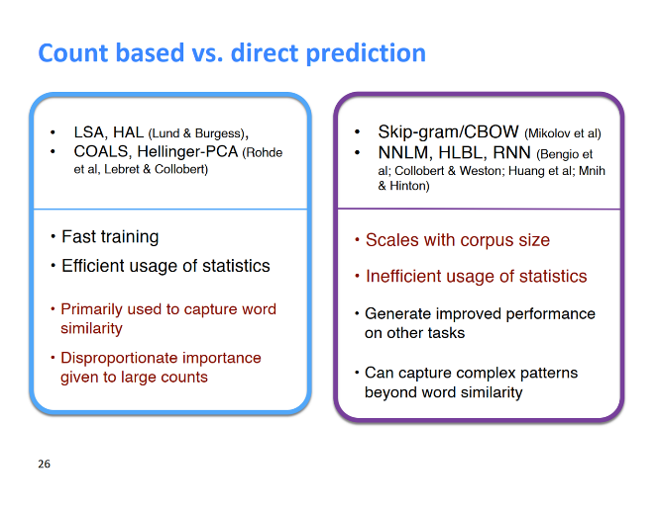
首先要说明，这2种方法输出的word embedding 都是distributed representation(稠密表达)。

其次值得说的是，这2种方法各有优缺点（可能面试里会问），在glove方法中，综合进行了两种算法，达到最优的效果。

那么，我们这里详细探讨一下利用SVD生成词向量的过程，解答上面提到的问题。

共现矩阵奇异值分解后为什么是用U的行来做word embedding

1.生成共现矩阵（Window based Co-occurrence Matrix）

构造一个矩阵X，这个矩阵的大小是 $V*V$ ，这里V是词表的长度。这个矩阵称之为共现矩阵。

我们要统计，每个中心词在左右k个窗口的范围内，上下文词出现的词频。于是这里的共现矩阵，第一个维度（列），代表这个中心词，第二个维度（行）代表这个中心词对应的上下文词。
$X={x_{ij}}$为第i个词作为中心词时，对应第j个词作为其上下文词时候的词频。

我们还是用课上的例子，有3句话：

1
2
3
I enjoy flying。
I like NLP。
I like deep learning。

假设这里k=1，统计的共现矩阵X为：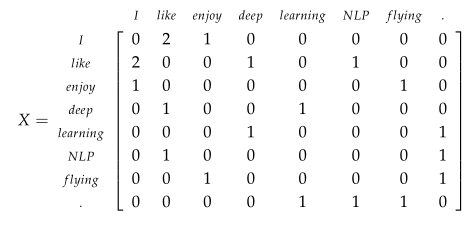

可以看出，这里的共现矩阵X为对称矩阵，也就是对中心词like，enjoy的出现次数是等于对于中心词enjoy，like的出现次数。

2.SVD分解的过程

假设X的size是$VV$,那么U的矩阵是$VK$,奇异值矩阵S是$KK$,而$V^T$的矩阵size 是$KV$.
这里V是词表长度，上面解释了，K是指最后需要输出的词向量维度，一般我们取100-300之间的一个值。

SVD分解公式可以写作
$X=USV^T$
写成分量式为：

$x_{ij}= \sum_{k=1}^n u_{ij}s_kv_{jk}$

那么从这个公式看出，对于每个样本word $x_{ij}$ 与$u_{ij}$是对于的，而不是与$v^T_j$对应，$v^T_j$与每个维度对应。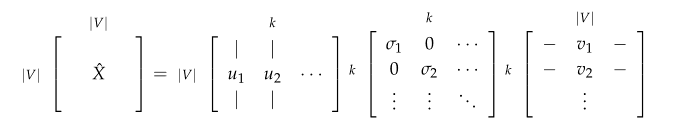

这里需要解释一下我们是如何得到SVD分解公式的：

由线性代数基本知识可知，对于任意矩阵X（size $V*V$ ）来说，我们可以进行奇异值分解，

$X=U \Lambda V^T$，

这里， $U, V, \Lambda$都是size $V*V$ 的对角矩阵，并且每个值都是非负实数，按大小从大到小排列。

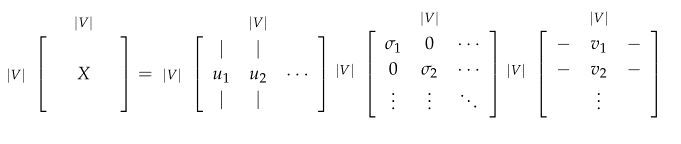
那么我们对$\Lambda$进行降维，只保留前K个值，这样U和V也会跟着变，从维度上看，矩阵U去掉了后面的一些列，变成了$VK$;矩阵$V^T$，去掉了前面的一些行，变成了$KV$（实质上做了空间变换，而不是简单的去除一些数据）。也就是上面的图：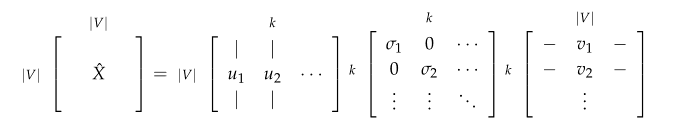

这里就解释了，为什么是用U的行来做word embedding。

3.如果U对应的词向量，那么V对应的是什么呢？

还有一个问题，如果U对应的词向量，那么V对应的是什么呢？对于词共现矩阵来说，V的意义还不是很清晰，我们考虑这样一个矩阵：

词-文档矩阵 Word-Document Matrix，行是所有的词，维度为V，列是每个文档，维度为M。

对这样一个矩阵进行SVD分解，并降维到K个奇异值上取值，

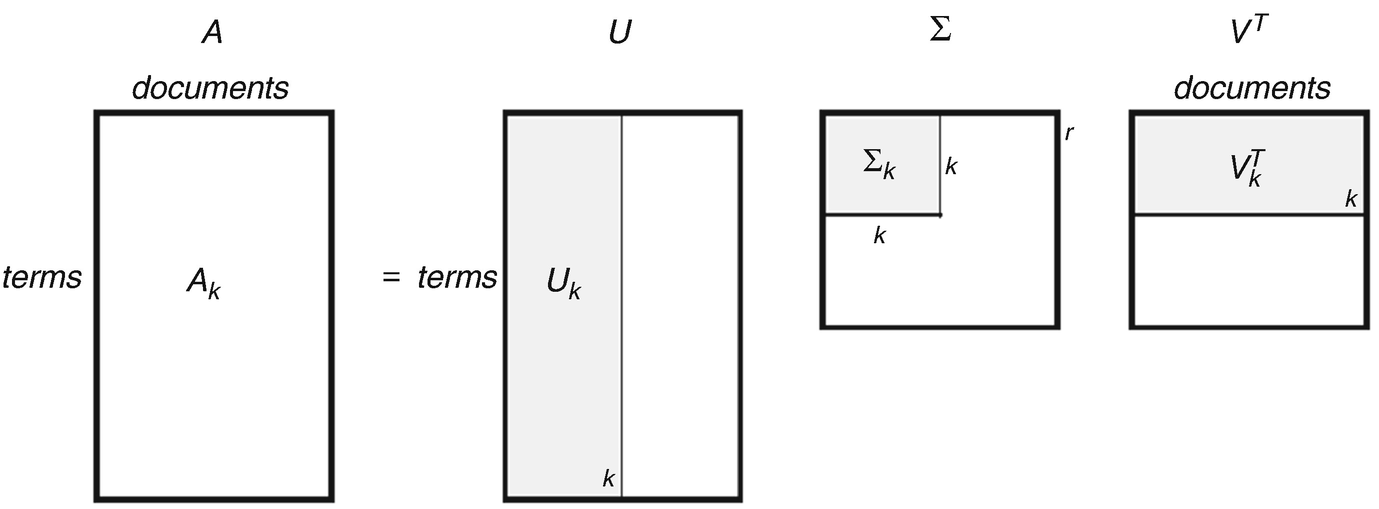
SVD分解公式可以写作
$X=U\Sigma V^T$

U的矩阵size$V*K$,

$V^T$的矩阵size 是$K*V$

写成分量式为：

$x_{ij}= \sum_{k=1}^n u_{ij}\sigma_kv_{jk}$

$u_{ij}$ 对应的第i个词和第j个主题的相关度，$u_{i}是词的主题向量$。

$v_{jk}$ 对应第j个文档和第k个主题的相关度，所以$v_j$是第j个文档的文档向量。

这样就说明了V在SVD分解的意义。